MathLab is more than just a computational tool—it’s a comprehensive platform designed to make complex mathematical operations accessible and straightforward. Whether you’re tackling high-level calculus, analyzing systems with Laplace transforms, or simply exploring the behavior of mathematical functions, MathLab has you covered.

A Deep Dive into MathLab’s Features:

-MathLab provides a suite of differentiation tools that cater to various analytical needs:

– Symbolic Differentiation: For exact results, MathLab offers symbolic differentiation, which directly computes the derivative of the function as an algebraic expression.
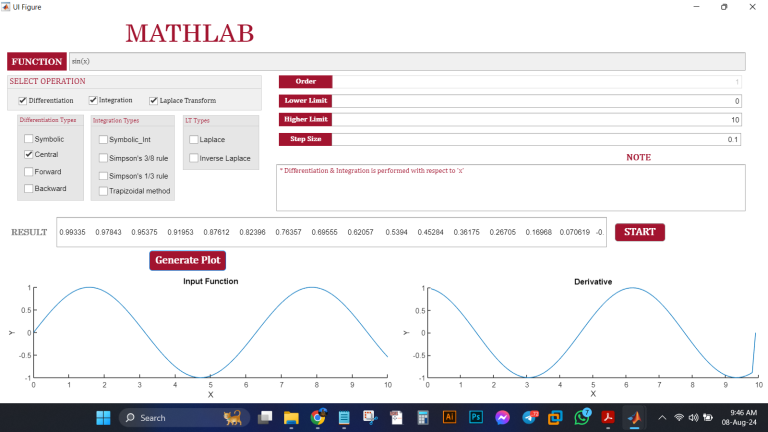
– Numerical Methods: Choose from central, forward, and backward difference methods to approximate derivatives, making MathLab ideal for analyzing functions where symbolic differentiation is difficult or unnecessary.

-Integration is at the heart of many mathematical analyses, and MathLab excels in this area:
– Symbolic Integration: Achieve exact solutions for integrals with MathLab’s symbolic integration feature. This is perfect for those looking to derive a function’s antiderivative or evaluate definite integrals with precision.
– Numerical Integration: MathLab includes a range of numerical methods such as:
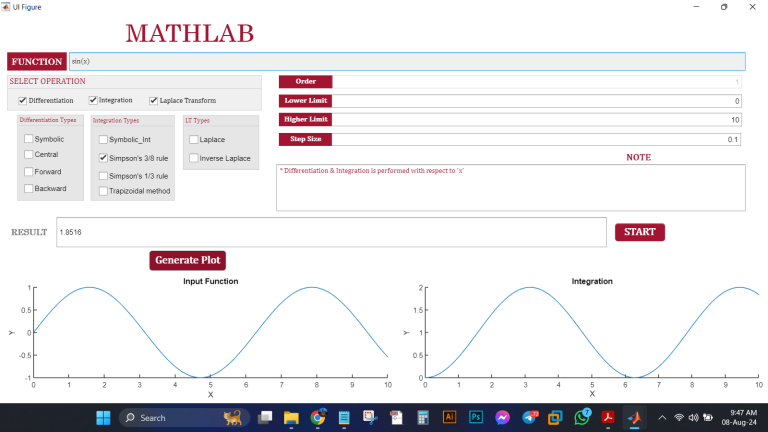
– Simpson’s 3/8 Rule: Ideal for situations where high accuracy is needed, especially when the function is complex or irregular.
– Simpson’s 1/3 Rule: A highly effective method for functions that are well-behaved and smooth.
– Trapezoidal Method: A versatile and straightforward technique for approximating the area under a curve, particularly useful for less smooth functions.

-MathLab simplifies the process of working with Laplace transforms, which are essential for solving differential equations and analyzing linear time-invariant systems:
– Laplace Transform: Transform your time-domain functions into the s-domain effortlessly, opening up a world of possibilities in system analysis and control theory.
– Inverse Laplace Transform: Convert your s-domain functions back to the time domain with ease, facilitating the interpretation of results in their original context.

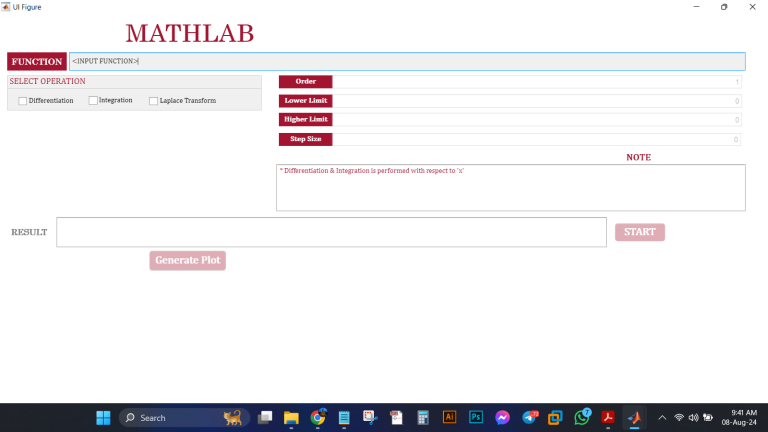
-MathLab is designed with the user in mind. The interface is clean, intuitive, and highly responsive, ensuring that you can focus on your work rather than the tool itself. Key features include:

– Interactive Input Fields: Easily input your functions and customize parameters such as order, lower and upper limits, and step size for numerical methods.
– Real-Time Results: Get immediate feedback with results displayed as soon as you hit the “START” button.
– Customizable Plots: MathLab not only computes but also visualizes. Generate detailed plots of both the input function and its differentiated or integrated form, helping you to visualize the mathematical behavior and understand the results at a glance.

-MathLab is versatile enough to be useful in various fields, including:

– Education: An invaluable tool for students and educators alike, MathLab helps demystify complex concepts in calculus, differential equations, and beyond.
– Engineering: Engineers can use MathLab to perform quick calculations, analyze systems, and solve real-world problems efficiently.
– Research: Academics and researchers benefit from MathLab’s accuracy and the ability to handle sophisticated mathematical tasks, enabling groundbreaking work in mathematics and applied sciences.

Why MathLab Stands Out?

– Precision and Accuracy: MathLab’s advanced algorithms ensure that your calculations are not only correct but also reliable.
– Versatility: Whether you need exact symbolic solutions or fast numerical approximations, MathLab provides the tools you need.
– Visualization: MathLab’s plotting capabilities allow you to see the bigger picture, making it easier to interpret and present your findings.
– Ease of Use: No need for extensive training or expertise—MathLab’s interface is designed to be intuitive and accessible to users of all levels, from beginners to professionals.